7章 スカラー3重積
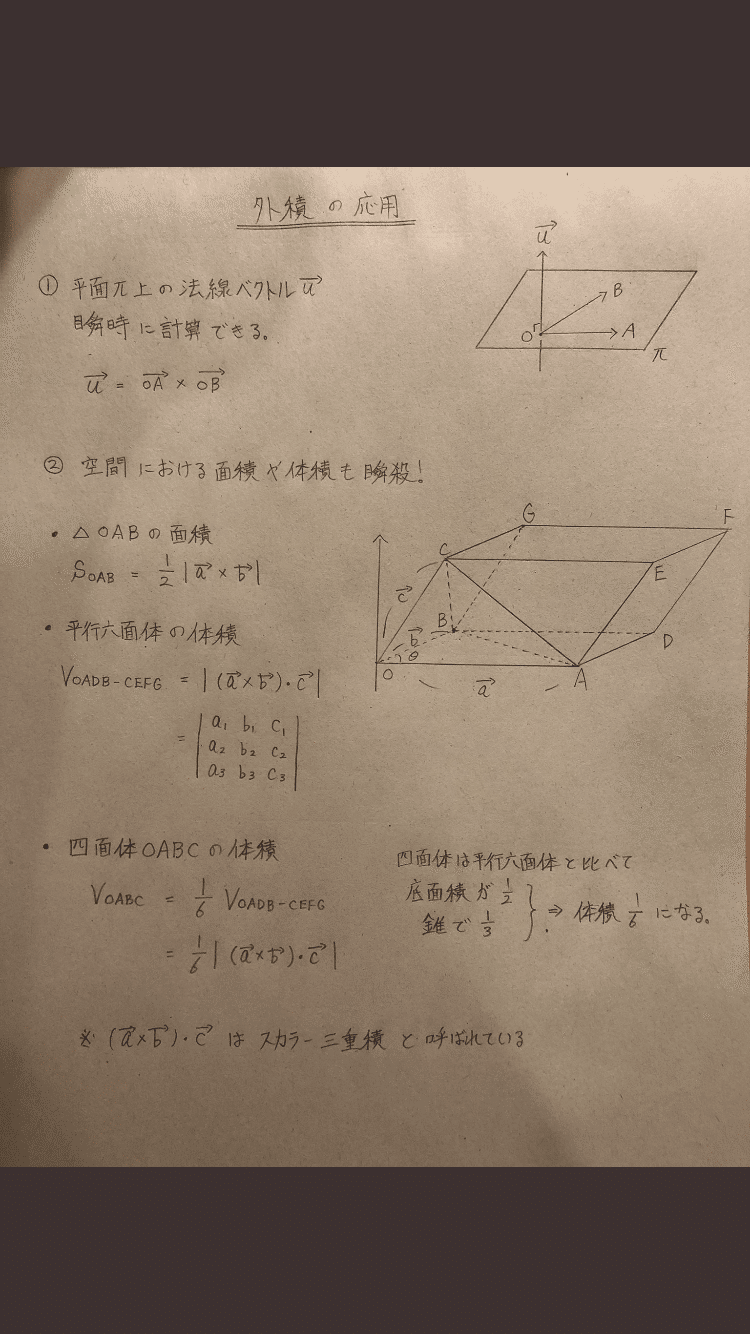
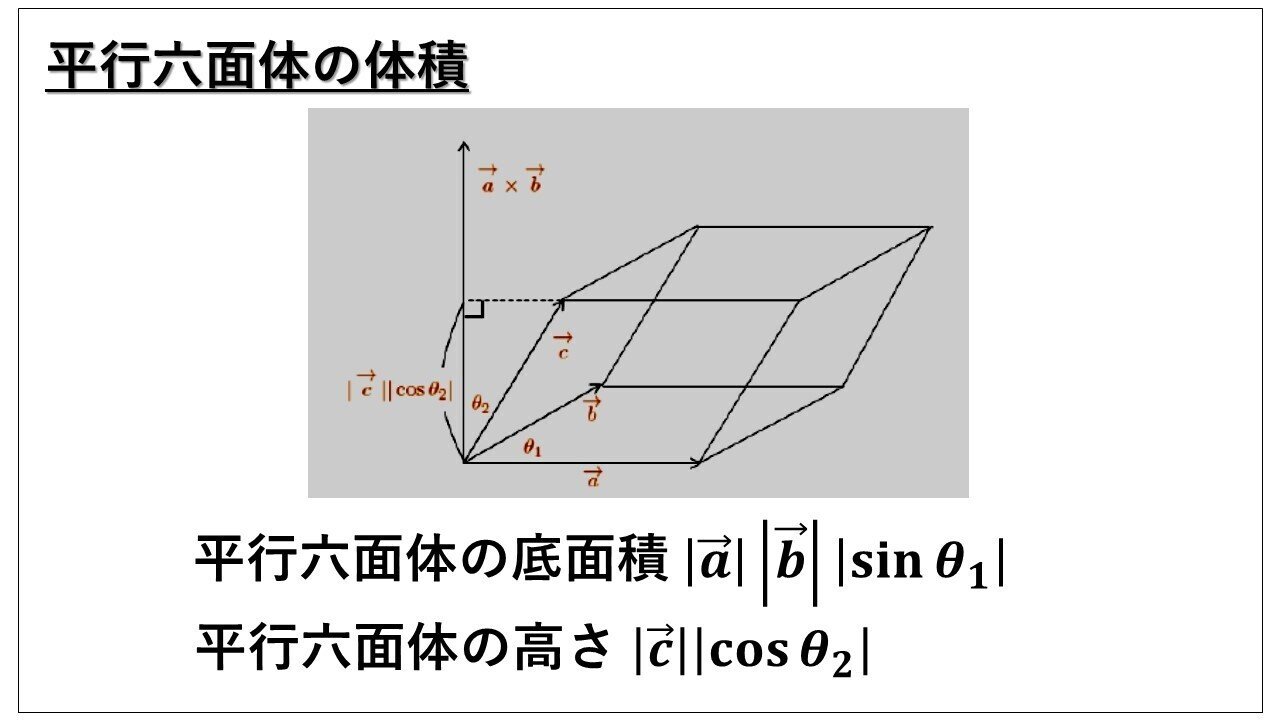
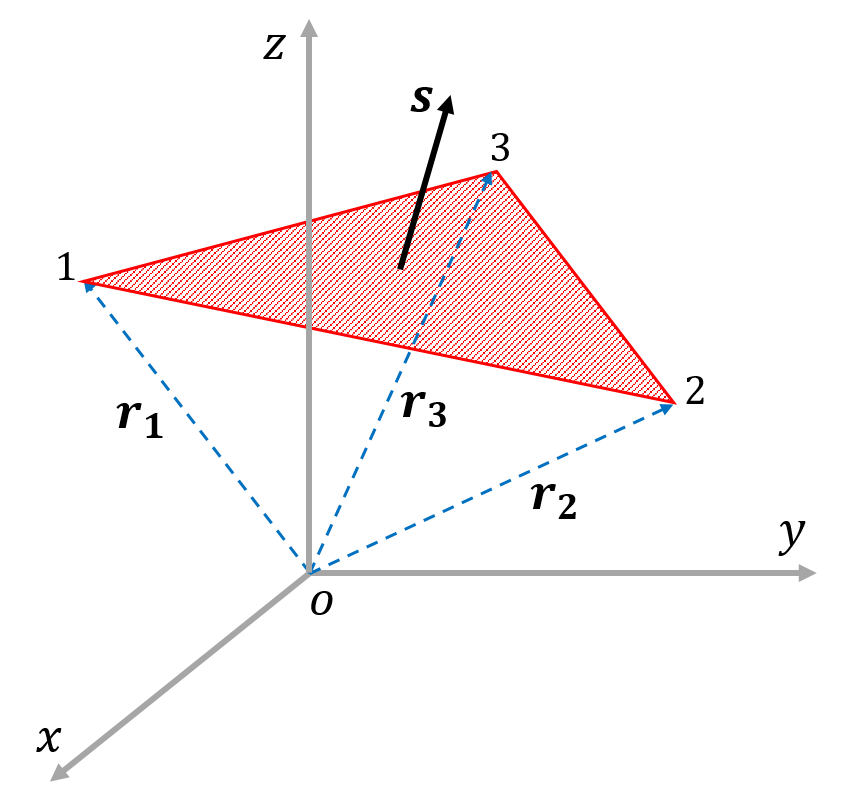
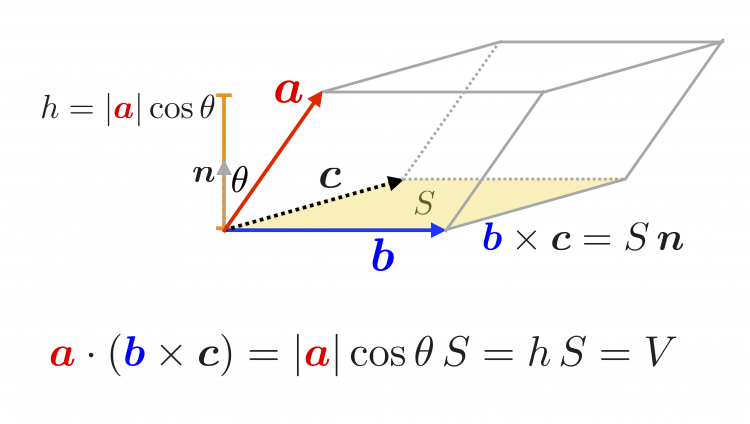
ベクトルの大きさの計算 と となる.この式からわかるようにスカラー3重積は,それぞれのベクトルが作る並行6面 体の体積になっている.ただし,スカラー3重積が負にもなるので注意が必要でベクトルの要素をクロスさせて計算 個人的に一番使う外積計算の方法ですかね。 高校生の時に学校の先生に教わった記憶があって、それ以来ずっと使っています。 2つのベクトルの成分をクロスして
ベクトル 体積 計算
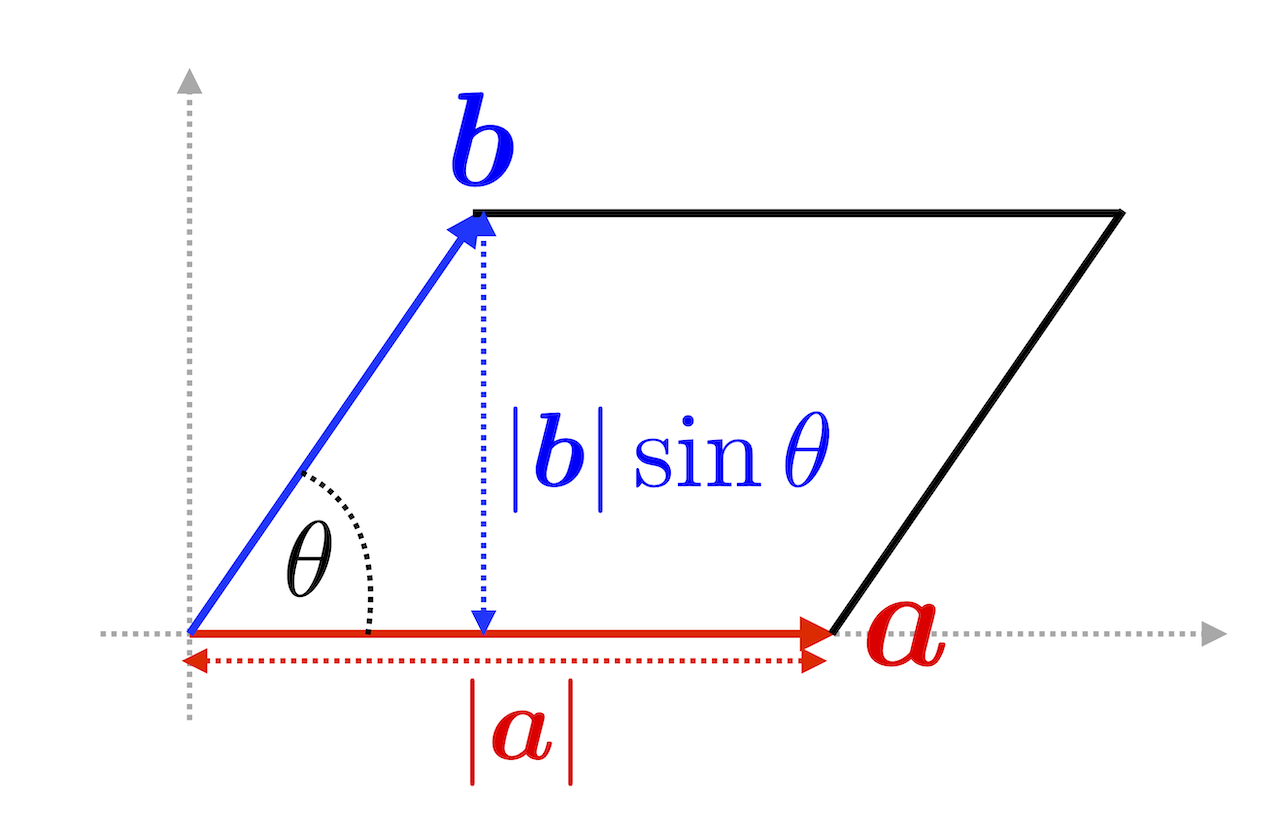
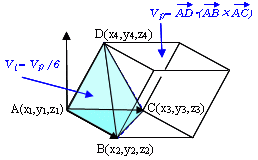
ベクトル 体積 計算- なんと, 3つのベクトルが張る平行六面体の体積は成分を並べた3×3の行列式として計算できるのだ ここで, 2つのベクトルが張る平行四辺形の符号付き面積が次の式で表せることを思 公式や証明、計算問題 21年12月30日 この記事では、ベクトルを使った三角形の面積の公式と求め方をできるだけわかりやすく解説していきます。 公式の証明や計算問題もていね

モデルの体積を計算する 試行錯誤
オンラインベクトル計算機。 ベクトルの外積、内積、ベクトルの加算と減算、ベクトル間の角度、大きさ、長さ、独立性、正規化、直交を見つける mxn calc 2 ベクトルの外積の計算方法 ベクトルの外積の幾何学的な意味を理解したところで、次にその求め方について見ていきましょう。 ここでは、そのための公式と、なぜこの公式でベク ベクトル関数 の微分計算は成分になっている関数を微分してあげるだけだった。 ベクトル関数の微分 成分が関数であるベクトルを "ベクトル関数" と言い、ベクトル関数の微分はそれ
ベクトルは,数値あるいは記号値の簡単なリストからなる n 次元ベクトル空間内のオブジェクトです. WolframAlphaは,ベクトルを球座標系あるいは極座標系に変換し,ベクトル長や正規化等のベProduct ベクトルの内積abは、aとbが同じ次元の場合のみ乗算が可能です。 ベクトルの外積a×bは、aとbが3次元の場合のみ乗算が可能です。 inner product a⋅b =c お客様の声 アンケート投稿体積積分の変数変換 ∫ V f ( u, v, w) d v = ∫ V ― f ― ( α, β, γ) d v ― となり、体積積分も変数変換で変わらない。 d v は微小な体積を表しており、単位を m 3 とすると、スカラー場 f ( x) は「単位
ベクトル 体積 計算のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  | |
「ベクトル 体積 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「ベクトル 体積 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「ベクトル 体積 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「ベクトル 体積 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「ベクトル 体積 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「ベクトル 体積 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「ベクトル 体積 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「ベクトル 体積 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「ベクトル 体積 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「ベクトル 体積 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 | ||
「ベクトル 体積 計算」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |





0 件のコメント:
コメントを投稿